Notacja Denavita-Hatenberga – polega ona na związaniu z każdym przegubem lokalnego układu współrzędnych, dzięki temu możemy wyliczyć kinematykę manipulatora. A jest to możliwe dzięki złożeniu tych transformacji.

Położenie układu współrzędnego. Zgodnie z zasadą notacji Denavita-Hatenberga oś powinna leżeć na osi łączącej człony manipulatora ze sobą. Natomiast oś powinna być prostopadła do osi pary członu.

Dopuszcza się następujące przekształcenia:

• Względem osi , obrót o kąt tak aby oś była równoległa do osi
• Względem osi , przemieszczenie o wielkość tak aby oś pokrywała się z osią
• Względem osi , przemieszczenie o wielkość aż początek układu współrzędnych będzie znajdował się w tej samej pozycji, czyli będzie się z nim pokrywał.
• Względem osi , obrót o kąt tak aby wszystkie osie układu współrzędnego pokryły się ze sobą.

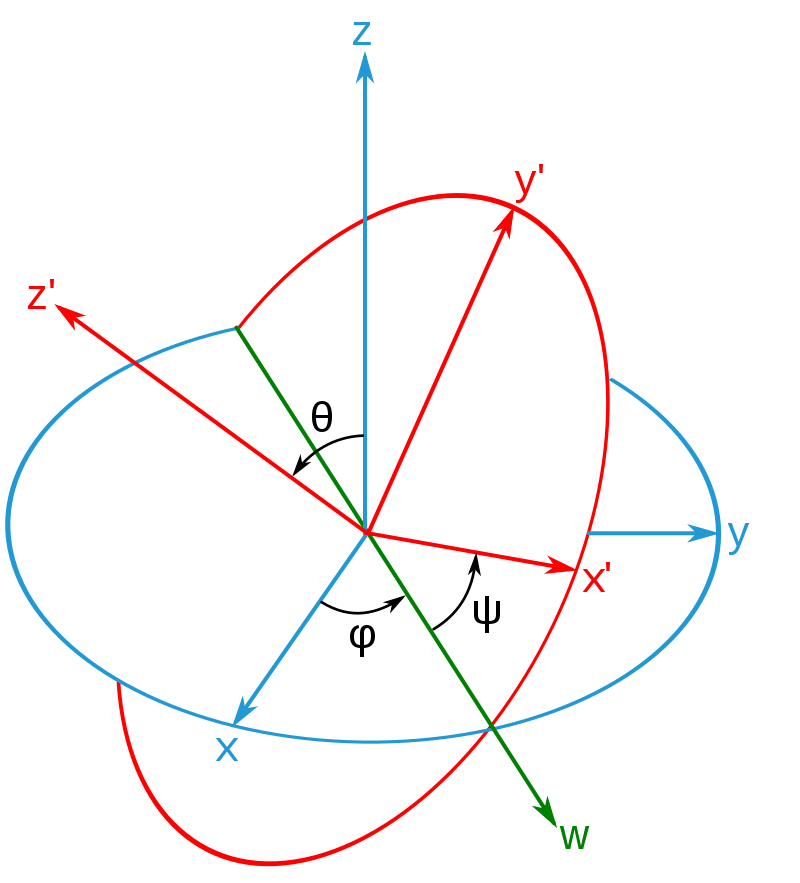
Notacji Eulera – polega na wzajemnym określeniu dwóch układów kartezjańskich, za pomocą trzech kątów. Układy kartezjańskie muszą być jednakowej skrętności w trójwymiarowej przestrzeni euklidesowej.

Położenie układu współrzędnego. Zgodnie z zasadami notacji Eulera układ współrzędnych można otrzymać z układu poprzez złożenie trzech obrotów wokół osi układu.

W pierwszej kolejności trzeba założyć że osi i nie są równoległe.

Dopuszcza się następujące przekształcenia:

• Względem osi z, obrót o kąt ϴ tak aby oś x pokrywała się z linią węzłów w
• Względem osi x (=w), obrót o kąt ϕ tak aby oś z pokrywała się z osią
• Względem osi z (= ), obrót o kąt ψ tak aby oś x pokrywała się z osią

Wtedy oś y okryje się z osią .

Różnice między Notacją Eulera a Notacją Denavita-Hatenberga:

Polega ona na ilości uwzględnianych czynników wpływających na względne położenie lokalnych układów współrzędnych. Jest tak ponieważ w notacji Eulera wykorzystuje się tylko kąty obrotu układów względem odpowiednich osi, natomiast w notacji Denavita-Hatenbergawykorzystuje się dodatkowo różnice odległości między osiami.

Notacja Denavita-Hatenberga, jest bardziej dokładniejsza ponieważ podczas jej obliczeń wykorzystuje się więcej czynników. Co powoduje dokładniejsze wyniki orientacji manipulatora w przestrzeni.

Bibliografia:

• John J. Craig „Wprowadzenie do robotyki: mechanika i sterowanie”
• T. Szkodny „Podstawy Robotyki”
• https://pl.wikipedia.org/wiki/K%C4%85ty_Eulera